3D Dynamic Scene Interpolation with Gaussian Splatting

In this project, we enhance the performance of Dynamic 3D Gaussian Splatting for sparse timewise inputs by introducing a loss term which integrates interpolated Gaussians from unseen timesteps. Detailed explanations of the project can be found in the downloadable paper on the upper right.

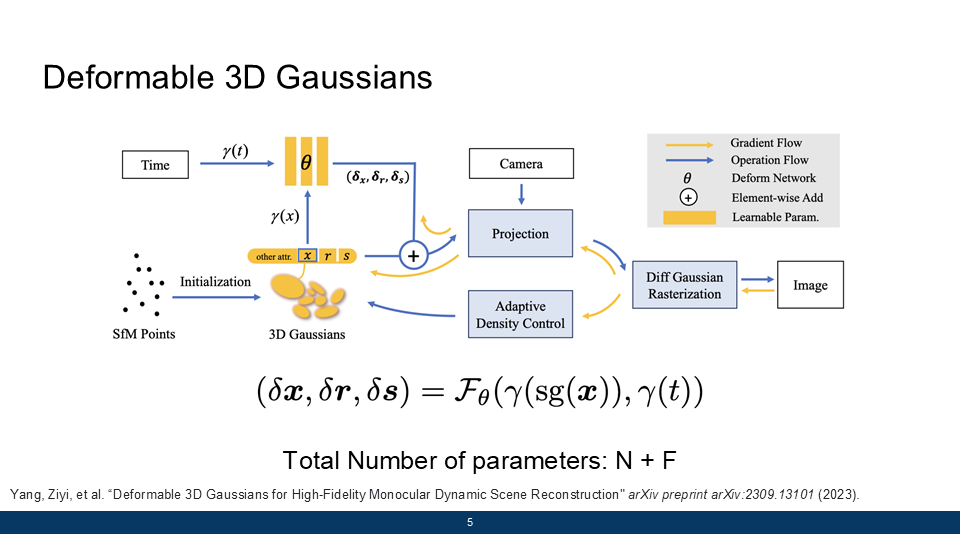
Gaussian Splatting is a method for representing a 3D scene with a large number of 3D Gaussians. In order to express a dynamic scene using 3D gaussians, the conventional approach is to generate an independent set of Gaussians for every timestep. However, this method requires a large amount of data and compuatational resources, which is inefficient. Deformable 3D Gaussians, or 4D Gaussian Splatting uses a MLP to solve this issue. In this approach, a trained MLP takes the initial Gaussian as its input, and returns the Gaussian at time t, which greatly reduces the number of parameters.

The biggest downside of 4D Gaussians Splatting is that the network is strongly overfitted to the input images, resulting in broken images at timesteps without any ground truth, which we refer to as interpolated timesteps.

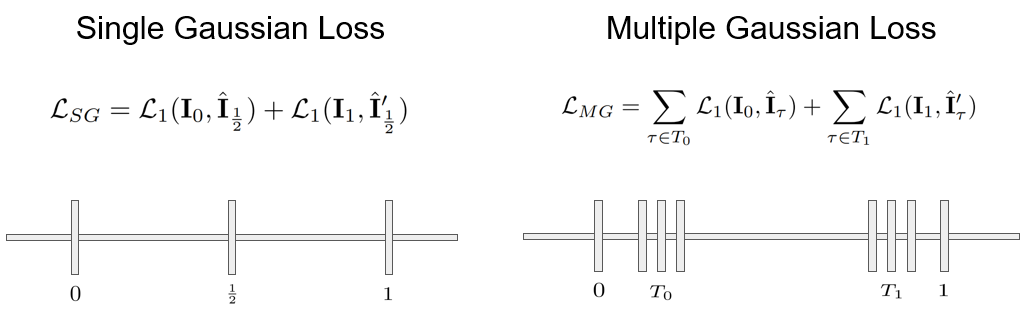
In order to address this issue, we propose Blended Gaussian Loss, which penalizes deviations between the scenes at interpolated timesteps and the ground truth. This loss term forces each interpolated scene to resemble one of the ground truth images, guiding the network to produce more realistic images.

The proposed method slightly outperforms vanilla 4D Gaussian Splatting, generating figures with less artifacts at timesteps without ground truth.